Good time of the day! The Quicktoken team is on, and today we’re going to talk about the task of generating packages. What does it consist of?
The optimal portfolio sale task

March 4
10K

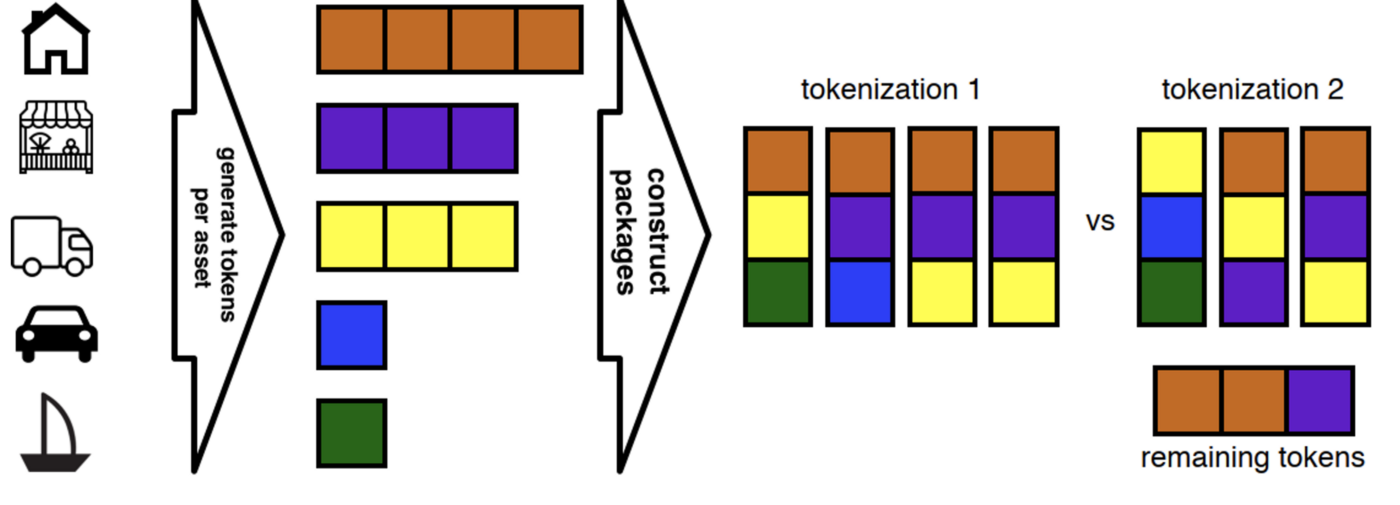

Let’s start with an example. Let the portfolio consist of N=5 initial assets and tokenized in the first step. The tokens have the same unit value. Each asset corresponds to a unique type of token and has its own issue. The tokens are then bundled into packages of k=3 pieces of different types in two ways — tokenization 1 and 2. The first one used all the initial tokens and the second one left three tokens without packages. So, using the first method of tokenization one can sell the entire portfolio in packages (hence the name — the problem of optimal portfolio sale), while the second method will fail to attract investors for the remaining three tokens and the portfolio owner will have to raise funds from other sources and bear the risk of the remaining tokens himself.
So how is the optimal sale of a portfolio formulated? We will write any tokenization in the form of a matrix (table). Rows are assets, columns are packages. The intersection of a row and a column is the amount of a given asset in the given package. Not every matrix is a tokenization: it is necessary that
- sums in each column have a given value, e.g. three
- sum in rows should not exceed the size of a corresponding asset in the initial portfolio
- the risk of each column was not higher than a given value, e.g. each package used a token from three different assets.
Thus, tokenization 2 is presented as a matrix below.
So how is the optimal sale of a portfolio formulated? We will write any tokenization in the form of a matrix (table). Rows are assets, columns are packages. The intersection of a row and a column is the amount of a given asset in the given package. Not every matrix is a tokenization: it is necessary that
- sums in each column have a given value, e.g. three
- sum in rows should not exceed the size of a corresponding asset in the initial portfolio
- the risk of each column was not higher than a given value, e.g. each package used a token from three different assets.
Thus, tokenization 2 is presented as a matrix below.
The optimal portfolio sale task is to find a tokenization matrix with as many columns as possible. In other words, we mean generating the maximum number of packages with given parameters from a given portfolio.
Much of the tokenization problem depends on the parameters:
- Can fractional numbers be used in the tokenization matrix?
- Are the assets in the portfolio correlated (dependent)?
We will discuss particular cases of the tokenization problem and algorithms for solving it in future issues. Next time, we will talk in detail about issuing token packages on the platform.
Much of the tokenization problem depends on the parameters:
- Can fractional numbers be used in the tokenization matrix?
- Are the assets in the portfolio correlated (dependent)?
We will discuss particular cases of the tokenization problem and algorithms for solving it in future issues. Next time, we will talk in detail about issuing token packages on the platform.

Twitter


