Доброе время суток! Команда Quicktoken работает, и сегодня мы поговорим о задаче генерации пакетов. Из чего он состоит?

Оптимальная задача продажи портфеля

10K
Март 4

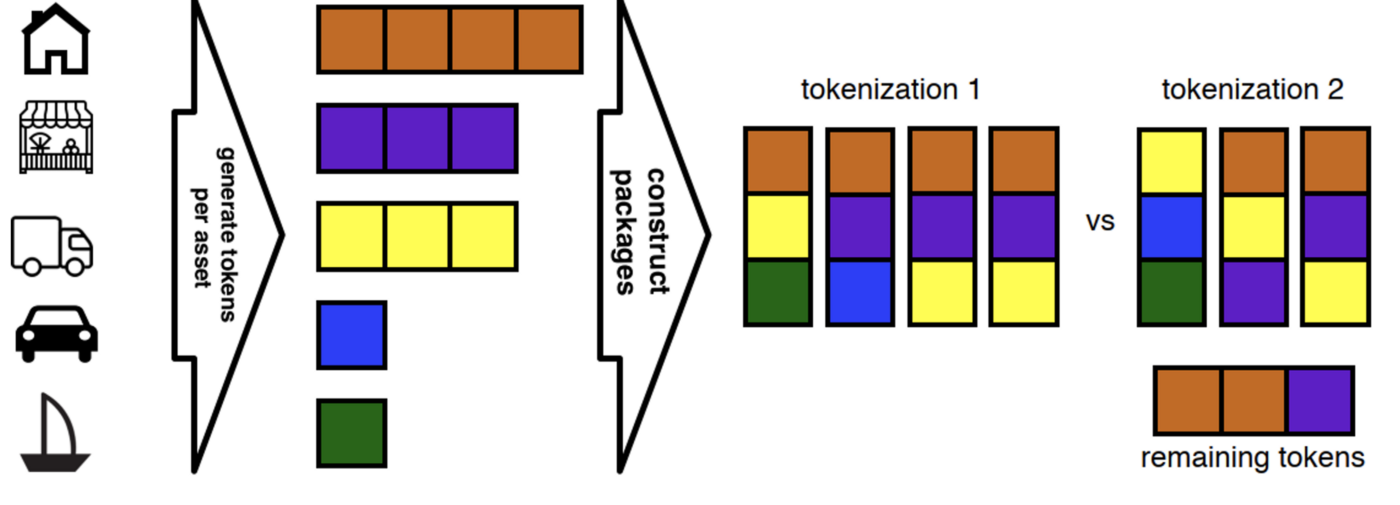
Начнем с примера. Пусть портфель состоит из N=5 начальных активов и токенизирован на первом этапе. Токены имеют одинаковую стоимость единицы. Каждый актив соответствует уникальному типу токена и имеет свою эмиссию. Затем токены объединяются в пакеты из k=3 штук разных типов двумя способами — токенизация 1 и 2. В первом использовались все исходные токены, а во втором оставались три токена без пакетов. Так, при первом способе токенизации можно продать весь портфель пакетами (отсюда и название — задача оптимальной продажи портфеля), а второй способ не привлечет инвесторов за оставшиеся три токена и владельцу портфеля придется привлекать средства из других источников и нести риск оставшихся токенов самостоятельно.
Так как же формулируется оптимальная продажа портфеля? Любую токенизацию запишем в виде матрицы (таблицы). Строки — это активы, столбцы — это пакеты. Пересечение строки и столбца — это количество данного актива в данном пакете. Не всякая матрица является токенизацией: необходимо, чтобы
- суммы в каждом столбце имели заданное значение, например три
- сумма в строках не должна превышать размер соответствующего актива в исходном портфеле
- риск каждого столбца не превышал заданного значения, т.е. в каждом пакете использовался токен из трех разных активов.
Таким образом, токенизация 2 представлена в виде матрицы ниже.
Так как же формулируется оптимальная продажа портфеля? Любую токенизацию запишем в виде матрицы (таблицы). Строки — это активы, столбцы — это пакеты. Пересечение строки и столбца — это количество данного актива в данном пакете. Не всякая матрица является токенизацией: необходимо, чтобы
- суммы в каждом столбце имели заданное значение, например три
- сумма в строках не должна превышать размер соответствующего актива в исходном портфеле
- риск каждого столбца не превышал заданного значения, т.е. в каждом пакете использовался токен из трех разных активов.
Таким образом, токенизация 2 представлена в виде матрицы ниже.
Задача оптимальной продажи портфеля — найти матрицу токенизации с максимально возможным количеством столбцов. Другими словами, имеется в виду генерация максимального количества пакетов с заданными параметрами из заданного портфеля.
Большая часть проблемы токенизации зависит от параметров:
- Можно ли использовать дробные числа в матрице токенизации?
- Являются ли активы в портфеле коррелированными (зависимыми)?
Частые случаи проблемы токенизации и алгоритмы ее решения мы обсудим в следующих выпусках. В следующий раз мы подробно поговорим о выпуске пакетов токенов на платформе.
Большая часть проблемы токенизации зависит от параметров:
- Можно ли использовать дробные числа в матрице токенизации?
- Являются ли активы в портфеле коррелированными (зависимыми)?
Частые случаи проблемы токенизации и алгоритмы ее решения мы обсудим в следующих выпусках. В следующий раз мы подробно поговорим о выпуске пакетов токенов на платформе.

Twitter


